Press Release

16 October 1985

The Royal Swedish Academy of Sciences has decided to award the Nobel Prize in Physics for 1985 to Professor Klaus von Klitzing, Max-Planck-Institute for Solid State Research, Stuttgart, Federal Republic of Germany, for the discovery of the quantized Hall effect.

 

Summary

When an electric current passes through a metal strip there is normally no difference in potential across the strip if measured perpendicularly to the current. If however a magnetic field is applied perpendicularly to the plane of the strip, the electrons are deflected towards one edge and a potential difference is created across the strip. This phenomenon, termed the Hall effect, was discovered more than a hundred years ago by the American physicist E.H. Hall. In common metals and semiconductors, the effect has now been thoroughly studied and is well understood.

Entirely new phenomena appear when the Hall effect is studied in twodimensional electron systems, in which the electrons are forced to move in an extremely thin surface layer between for example a metal and a semiconductor. Two-dimensional systems do not occur naturally, but, using advanced technology and production techniques developed within semiconductor electronics, it has become possible to produce them.

For the last ten years there has been reason to suspect that, in two-dimensional systems, what is called Hall conductivity does not vary evenly, but changes "step-wise" when the applied magnetic field is changed. The steps should appear at conductivity values representing an integral number multiplied by a natural constant of fundamental physical importance. The conductivity is then said to be quantised.

It was not expected, however, that the quantisation rule would apply with a high accuracy. It therefore came as a great surprise when in the spring of 1980 von Klitzing showed experimentally that the Hall conductivity exhibits step-like plateaux which follow this rule with exceptionally high accuracy, deviating from an integral number by less than 0.000 000 1.

Von Klitzing has through his experiment shown that the quantised Hall effect has fundamental implications for physics. His discovery has opened up a new research field of great importance and relevance.

Because of the extremely high precision in the quantised Hall effect, it may be used as a standard of electrical resistance. Secondly, it affords a new possibility of measuring the earlier-mentioned constant, which is of great importance in, for example, the fields of atomic and particle physics. These two possibilities in measurement technique are of the greatest importance, and have been studied in many laboratories all over the world during the five years since von Klitzing's experiment. Of equally great interest is that we are dealing here with a new phenomenon in quantum physics, and one whose characteristics are still only partially understood.

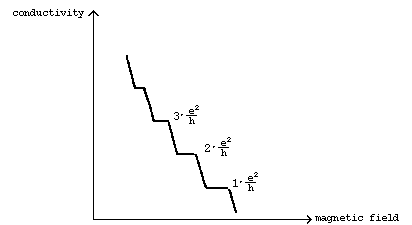
Conductivity changes "step-wise" when the magnetic field is changed. The conductivity is said to be quantised.

 

Background information

The Movement of Electrons in Magnetic Fields
Under the influence of a magnetic field an electron in a vacuum follows a spiral trajectory with the axis of the spiral in the direction of the magnetic field. In the plane perpendicular to the field, the electron moves in a circle. In a metal or a semiconductor, the electron tends to move along a more complicated closed trajectory, but with fairly strong magnetic fields and at normal temperatures this ordered movement is fragmented by collisions. At extremely low temperatures (a few degrees above absolute zero) and with extremely strong magnetic fields, the effect of collisions is suppressed and the electrons are again forced into ordered movement. Under these extreme conditions the classical theory does not apply: the movement becomes quantised, which means that the energy can only assume certain definite values, termed Landau levels after the Russian physicist L. Landau (Nobel prizewinner in 1962) who developed the theory of the effect as early as 1930.

Two-dimensional Electron Systems
Two-dimensional material systems do not occur naturally. Under special circumstances, however, certain systems can behave as if they were two-dimensional - but only within very limited energy intervals and temperature ranges. The first to demonstrate this possibility theoretically was J.R. Schrieffer (Nobel prizewinner in 1972). In work appearing in 1957 he showed that in a surface layer between metal and semiconductor electrons can be made to move along the surface but not perpendicular to it. Eleven years later a research team at IBM showed that this idea could be realised experimentally. The study of two-dimensional systems developed rapidly during the years that have followed.

These experiments used samples employing a specially designed transistor, a so called MOSFET (Metal-Oxide-Semiconductor Field Effect Transistor). Other types of artificial samples - heterostructures - have subsequently been used, in which the samples have been developed using molecular beams.

It should also be mentioned that advances in technology and production methods within semiconductor electronics have played a crucial role in the study of two-dimensional electron systems, and were a precondition for the discovery of the quantised Hall effect.

The Quantised Hall Effect
An important step in the direction of the experimental discovery was taken in a theoretical study by the Japanese physicist T. Ando. Together with his co-workers he calculated that conductivity could at special points assume values that are integer multiples of e² /h, where e is the electron charge and h is Planck's constant. It could scarcely be expected, however, that the theory would apply with great accuracy.

During the years 1975 to 1981 many Japanese researchers published experimental papers dealing with Hall conductivity. They obtained results corresponding to Ando's at special points, but they made no attempt to determine the accuracy. Nor was their method specially suitable for achieving great accuracy.

A considerably better method was developed in 1978 by Th. Englert and K. von Klitzing. Their experimental curve exhibits well defined plateaux, but the authors did not comment upon these results. The quantised Hall effect could in fact have been discovered then.

The crucial experiment was carried out by Klaus von Klitzing in the spring of 1980 at the Hochfelt-Magnet-Labor in Grenoble, and published as a joint paper with G. Dorda and M. Pepper. Dorda and Pepper had developed methods of producing the samples used in the experiment. These samples had extremely high electron mobility, which was a prerequisite for the discovery.

The experiment clearly demonstrated the existence of plateaux with values that are quantised with extraordinarily great precision. One also calculated a value for the constant e² /h which corresponds well with the value accepted earlier. This is the work that represents the discovery of the quantised Hall effect.

Following the original discovery, a large number of studies have been carried out that have elucidated different aspects of the quantised Hall effect. The national metrological (measurement) laboratories in Germany, the USA, Canada, Australia, France, Japan and other countries have carried out very detailed investigations of the precision of the quantisation, in order to be able to use the effect as a standard.

A new and entirely unexpected discovery was made at the beginning of the 1980's when a research team at the Bell Laboratories found plateaux corresponding to the fractional numbers 1/3, 2/3, 4/3, 5/3, 2/5, 3/5, 4/5, 2/7..... multiplied by the constant e² / h. This was the discovery of the fractional quantum Hall effect. This concerns an entirely new type of quantum phenomenon, in which the movements of the different electrons are very strongly linked to each other. This effect is at present the subject of extensive experimental and theoretical studies.