Press Release

16 October 1991

The Royal Swedish Academy of Sciences has decided to award the 1991 Nobel Prize in Physics to Professor Pierre-Gilles de Gennes, College de France, Paris, France for discovering that methods developed for studying order phenomena in simple systems can be generalized to more complex forms of matter, in particular to liquid crystals and polymer.

Order and disorder in nature

This year's Laureate, the Frenchman Pierre-Gilles de Gennes, has described mathematically how e.g. magnetic dipoles, long molecules or molecule chains can under certain conditions form ordered states, and what happens when they pass from an ordered to a disordered state. Such changes of order occur when, for example, a heated magnet changes from a state in which all the small atomic magnets are Lined up in parallel to a disordered state in which the magnets are randomly oriented. The transition from disorder to order always occurs at a well-defined temperature and can sometimes also take place in jumps. There is a phase transition at a critical temperature, which in the case of ferro-magnets is termed the Curie temperature.

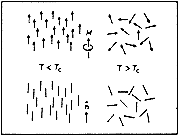
Fig 1a. Magnetic order

Fig 1b. Order in liquid crystals

Pierre-Gilles de Gennes began by working on magnetic phase transitions, but during the 1960s and 1970s studied other, more complicated, order phenomena The transition to a superconducting state in certain materials, from an ordered state to a disordered state in liquid crystals; regularities in the geometrical arrangement and movement of polymer chains; conditions of stability in micro-emulsions, and other phenomena: all these have been objects of de Gennes' interest. Some of these systems are so complicated that physicists had earlier been unable to discern general rules for how they behave during the transition from order to disorder. De Gennes has in many cases succeeded in doing this, in particular for liquid crystals and polymers. In addition, he has shown that phase transitions in such apparently widely-differing physical systems as magnets, superconductors, liquid crystals and polymer solutions can be described in mathematical terms of surprisingly broad generality.

Some examples of the laureate's contributions
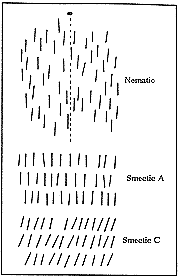
Liquid crystals have been known for over a century and their hydrodynamics, that is, how they flow, were studied as early as the 1920s by Professor Wilhelm Oseen of Uppsala. But it was not until the 1960s that the development of liquid crystals gathered impetus with the technical exploitation of their optical properties for showing numbers in pocket calculators, wristwatches, etc. Liquid crystals have been called "nature's delicate phase of matter" because the molecules can be arranged in many different, characteristic ways, and because the arrangement is also easily affected by weak electrical or magnetic fields. One of the ordered phases is the "nematic" phase, in which the molecules move as if in an ordinary three-dimensional liquid, but with their axes mainly pointing the same way. Other phases are termed "smectic" (i.e. soap-like), where the molecules can also flow, but only in two dimensions, in parallel layers. In industry, these properties have led to the optical applications mentioned, since liquid crystals are also optically active and alter the polarisation of light or scatter light strongly when it passes through thin layers of the crystals. Recently, "flat" TV screens have been described. These are based on the electro-optical properties of liquid crystals. In physics, on the other hand, liquid crystals are often seen mainly as an exciting "playground" where the arrangements which they assume can easily be modified and studied. In these cases liquid crystals can act as model systems for experiments to test more general theories.

At the end of the 1960s de Gennes formed the liquid crystal group in Orsay. This research team consisted of both experimenters and theorists. It quickly became one of the leading groups in the field. De Gennes himself made his chief contributions to our knowledge of liquid crystals when he explained what is termed anomalous light scattering from nematic liquid crystals. This light scattering depends in a complicated manner on fluctuations in the orientational order. Another important contribution was his description of the conditions for one of the transition points that occur when a weak alternating electric field is applied. In addition, de Gcnnes demonstrated important similarities between the behaviour of liquid crystals and that of superconductors. Published in 1974, his book 'The Physics of Liquid Crystals" has become a standard work.

Somewhat later de Gennes began to be interested in the conformation and dynamics of the polymers. Polymers are formed out of very long chains of simpler links, termed monomers. The links may be about 10 Ångstrom (i.e. 10^-7 cm) long, and the chains consist of tens of thousands of similar links. Polymer molecules in dilute solutions form loops, or "tangles", rather like spaghetti. When followed from end to end the winding-about appears like an (almost) random movement in three dimensions. Attempts had been made earlier to descnbe m mathematical-statistical terms the venous possibilities for the spatial disposition of the molecules, also taking into account the fact that a chain cannot have more than one link in the same place at the same time. The Englishman S.F. Edwards made important contributions in this area by introducing a technique of calculation taken from theoretical particle physics. De Gennes' important discovery was that there were far more similarities than had hitherto been suspected between this "order in disorder" in the arrangement of polymers and the conditions that apply when a system of magnetic moments moves from order to disorder. With this, de Gennes opened the way for new descriptions of complicated order phenomena in polymers, which are based on general physical principles of phase transition. In the "Orsay group", the descriptions were soon developed to apply also to polymers in more concentrated solutions, in which the various chains can partly "entangle" themselves, and in high concentrations in pure melts of polymers.

For the latter cases, de Gennes has also established a number of predictions regarding how polymer chains and their individual parts can move, i.e. what physicists call polymer dynamics. These predictions often have the character of "scaling laws": they say that conditions shall be similar for certain combinations of the starting variables (such as polymer concentration in a solution, and temperature). These are properties that can sometimes be controlled experimentally, and many works on polymer dynamics have been performed using neutron-scattering techniques. In experiments of this kind, it is possible to distinguish how individual parts of a polymer chain move by noting how an oscillation of a selected wavelength initiated by the neutron collision is damped during a certain measurable time. Such measurements have helped to confirm de Gennes' models for polymer-chain motion. One of these models, the "blob" model, states that a certain typical segment of a chain can move as if it were free, even in more concentrated solutions. Another is the "reptation" model, which describes the serpentine motion of a polymer chain within a "tangle" of surrounding polymer chains.

De Gennes formed a school for polymer studies as well, and gathered around him a large number of co-workers in STRASACOL a joint project with physicists and chemists from Strasbourg, Saclay and the College de France (to which de Gennes had then been appointed). His work in this field is described in his "Scaling Concepts in Polymer Physics", which came out in 1979. De Gennes has since contributed new viewpoints in many fields unconventional for physicists such as gels, porous media and other so-called soft systems.

Fig 2. The "blob" model

Pierre-Gilles de Gennes - a coordinator in physics
Pierre-Gilles de Gennes has by some judges been called "the Isaac Newton of our time". The reason for this highly appreciative epithet is probably that de Gennes has succeeded in perceiving common features in order phenomena in very widely differing physical systems, and has been able to formulate rules for how such systems move from order to disorder. Some of the systems de Gennes has treated have been so complicated that few physicists had earlier thought it possible to incorporate them at all in a general physical description. Physicists often take pride in dealing with systems that are as simple and "pure" as possible, but de Gennes' work has shown that even "untidy" physical systems can successfully be described in general terms. In this way he has opened new fields in physics and stimulated a great deal of theoretical and experimental work in these fields. While this is pure research, it has also meant the laying of a more solid foundation for the technical exploitation of the materials mentioned here: liquid crystals and polymers.