Pressmeddelande: Nobelpriset i fysik 1998
English
Swedish

13 oktober 1998
Kungl. Vetenskapsakademien har utdelat 1998 års Nobelpris i fysik gemensamt till
Professor Robert B. Laughlin, Stanford University, Kalifornien, USA,
Professor Horst L. Störmer, Columbia University, New York, och Lucent Technologies’ Bell Labs, New Jersey, USA, och
Professor Daniel C. Tsui, Princeton University, New Jersey, USA.
De tre forskarna Nobelprisbelönas för att ha upptäckt att elektroner i samverkan i starka magnetfält bildar en ny form av “partiklar” med laddningar som är bråkdelar av elektronens laddning.
Vetenskapsakademiens motivering:
“för deras upptäckt av en ny form av kvantvätska med fraktionellt laddade excitationer.”
Elektroner i ny skepnad
Horst L. Störmer och Daniel C. Tsui gjorde upptäckten 1982 i ett experiment, där de utnyttjade extremt starka magnetfält och låga temperaturer. Inom ett år efter upptäckten lyckades Robert B. Laughlin förklara deras resultat. Genom teoretisk analys visade han att elektronerna i ett starkt magnetfält kan kondensera och bilda en sorts kvantvätska, besläktad med de kvantvätskor som uppträder vid supraledning och i flytande helium. Det som gör dessa vätskor speciellt viktiga för forskarna är att skeenden i en droppe kvantvätska kan ge fördjupade insikter om materiens allmänna inre struktur och dynamik. De tre pristagarnas insatser har därmed lett till ännu ett genombrott i vår förståelse av kvantfysik och till utveckling av nya teoretiska begrepp av betydelse för flera grenar inom modern fysik.
Kvanteffekter blir synliga
Redan som ung student upptäckte amerikanen Edwin H. Hall 1879 ett oväntat fenomen. Han fann att om en tunn platta av guld befinner sig i ett magnetfält som riktats vinkelrätt mot plattans yta kan en elektrisk ström som flyter längs med plattan göra att det bildas en spänning vinkelrätt mot både strömmen och magnetfältet (se fig. 1). Denna så kallade Halleffekt beror på att elektriskt laddade partiklar (i detta fall elektroner) som rör sig i ett magnetfält påverkas av en kraft och böjer av åt sidan. Halleffekten kan bl.a. användas för att bestämma tätheten av laddningsbärare (negativa elektroner eller positiva hål) i både ledare och halvledare och har blivit ett standardverktyg i världens alla fysiklaboratorier.
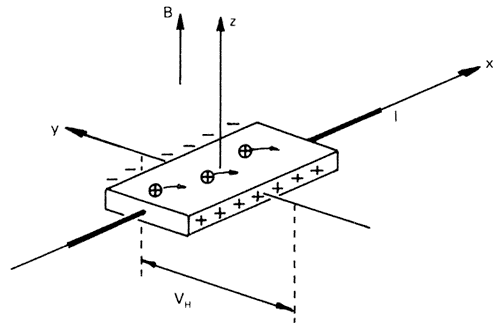 |
Fig. 1. En spänning V driver en ström I i positiva x-riktningen. Den vanliga Ohmska resistansen är V/I. Ett magnetfält i positiva z-riktningen förskjuter positiva laddningsbärare i negativa y-riktningen. Detta ger upphov till en Hallspänning ( VH) och en Hallresistans ( VH /I ) i y-riktningen (Kosmos 1986. Se litteraturförteckningen!)
Hall gjorde sina experiment vid rumstemperatur och med måttligt starka magnetfält, mindre än en tesla (T). I slutet av 1970-talet utnyttjade forskarna istället extremt låg temperatur (bara någon grad från absoluta nollpunkten, d.v.s. omkring -272° C) och mycket starka magnetfält (maximalt cirka 30 T). De studerade Halleffekten i samma slags halvledarkonstruktion som elektronikindustrin använder för att tillverka lågbrusiga transistorer. Materialet innehåller elektroner som är bundna i ett tunt skikt vid en yta som delar provet i två delar, men som trots detta är mycket lättrörliga inom skiktet.
I ett sådant skikt kan man vid låga temperaturer få elektroner att röra sig som på en plan yta, alltså i endast två dimensioner. Denna geometriska begränsning leder till många oväntade effekter. En av dessa är att Halleffekten ändrar karaktär. Enklast syns detta om man mäter hur den s.k. Hallresistansen (se ovanstående figurtext) beror av det pålagda magnetfältets styrka.
Den tyske fysikern Klaus von Klitzing upptäckte 1980 i ett liknande experiment att Hallresistansen inte varierar jämnt utan ändrar sig “trappstegsformat” då man ändrar magnetfältets styrka (se fig. 2). Trappstegen uppträder vid värden på resistansen som inte beror på materialets egenskaper utan som ges av en konstant av grundläggande fysikalisk betydelse dividerad med ett heltal. Man säger att resistansen är kvantiserad. Vid de kvantiserade värdena på Hallresistansen försvinner även den vanliga Ohmska resistansen och materialet blir i viss mening supraledande
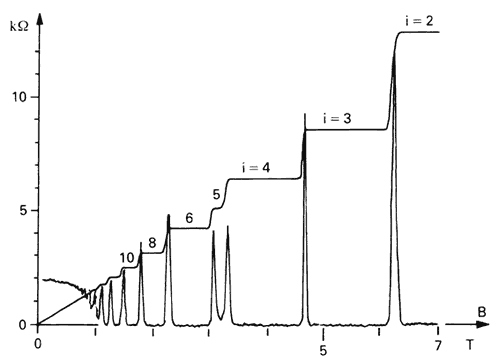
Fig. 2. Hallresistansen ändrar sig trappstegsformat då magnetfältet B ändras. Höjden på trappstegen ges av den fysikaliska konstanten h/e2 (vars värde är cirka 25 kilo-ohm) dividerad med ett heltal i. I figuren syns trappstegen för i = 2,3,4,5,6, 8 och 10. Effekten har gett upphov till en ny internationell standard för resistans. Sedan 1990 ges denna av enheten 1 klitzing, definierad som Hallresistansen vid det fjärde trappsteget (h/4e2). Den undre toppiga kurvan representerar den Ohmska resistansen, vilken försvinner vid varje trappsteg. (Kosmos 1986. Se litteraturförteckningen!)
För upptäckten av den så kallade heltalskvantiserade Halleffekten erhöll von Klitzing Nobelpriset i fysik 1985. Effekten kan förstås om man accepterar kvantfysikens lagar för hur enskilda elektroner uppför sig i ett starkt magnetfält. Enkelt uttryckt rör sig elektronerna endast i vissa givna cirkelbanor, vars grundstorlek bestäms av magnetfältet. De olika trappstegen visar sig tala om hur många av de minsta banorna som är helt fyllda av elektroner.
I sina förfinade experimentella studier av den kvantiserade Halleffekten, vilka bl.a. utnyttjade lägre temperaturer och högre magnetfält, fann Störmer, Tsui och deras medarbetare 1982 till sin stora förvåning ett nytt trappsteg i Hallresistansen vilket var tre gånger högre än von Klitzings högsta. Därefter fann de fler och fler nya trappsteg, både ovanför och mellan de heltaliga. Alla de nya trappstegens höjder kan uttryckas med samma konstant som tidigare, men nu dividerad med olika bråktal. Därför fick upptäckten namnet den bråktalskvantiserade Halleffekten. Den innebar ett stort mysterium för forskarna, som inte kunde förklara de nya trappstegens uppkomst.
En ny typ av kvantvätska
Ett år efter upptäckten av den bråktalskvantiserade Halleffekten kom Laughlin med en teoretisk förklaring. Enligt hans teori tvingar den låga temperaturen och det starka magnetfältet elektrongasen att kondensera till en helt ny typ av kvantvätska. Eftersom elektroner har den egenskapen att de inte alls vill kondensera (de är s.k. fermioner) slår de sig i viss mening först ihop med magnetfältets så kallade flödeskvanta. Speciellt för det trappsteg som Störmer och Tsui först upptäckte fångar elektronerna in tre flödeskvanta var och bildar därigenom ett slags sammansatta partiklar som inte har något emot att kondensera (de blir s.k. bosoner).
Kvantvätskor har ju tidigare visat sig uppträda vid mycket låga temperaturer i flytande helium (Nobelpris 1962 till Landau; 1978 till Kapitsa; 1996 till Lee, Osheroff och Richardson) och i supraledare (Nobelpris 1913 till Kamerlingh Onnes; 1972 till Bardeen, Cooper och Schrieffer; 1987 till Bednorz och Müller). Kvantvätskorna har vissa egenskaper gemensamma, t.ex. suprafluiditet, men det finns också viktiga skillnader i deras beteenden. Några av dem består liksom Laughlins vätska av sammansatta partiklar.
Den nya kvantvätska som Laughlin föreslog har, förutom den suprafluiditet vilken förklarar att den Ohmska resistansen försvinner på Hallresistansens trappsteg, många ovanliga egenskaper. En av de mest uppseendeväckande är att om en elektron adderas kommer vätskan att påverkas (exciteras) och ett antal bråktalsladdade så kallade kvasipartiklar uppstår. Dessa kvasipartiklar skall inte uppfattas som partiklar i vanlig mening utan som ett resultat av elektronernas gemensamma dans i kvantvätskan. Laughlin kunde först visa att dessa kvasipartiklar har precis den rätta bråktalsladdningen för att förklara Störmers och Tsuis resultat. Senare mätningar visar på allt fler bråktalsladdade trappsteg i Hallresistansen (se fig. 3). Laughlins kvantvätska har visat sig kunna förklara alla de trappsteg man funnit experimentellt.
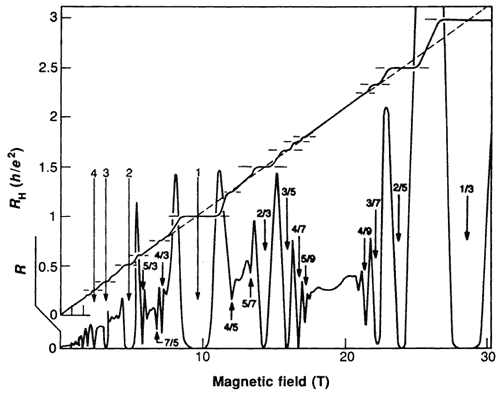 |
Fig. 3. Den streckade linjen som löper diagonalt representerar den klassiska Hallresistansen och den heldragna diagonala kurvan med trappsteg de experimentella resultaten. De magnetfält som ger upphov till trappsteg är markerade med pilar. Notera speciellt det av Störmer och Tsui först upptäckta trappsteget (1/3) vid det högsta värdet på magnetfältet och de av von Klitzing tidigare upptäckta trappstegen (heltal) vid svagare magnetfält. (Science 1990. Se litteraturförteckningen!)
Den nya kvantvätskan gör kraftigt motstånd mot att tryckas ihop och sägs vara inkompressibel. Detta beror på att den reagerar på komprimering genom att bilda fler kvasipartiklar, vilket kostar energi.
Direkt påvisande av kvasipartiklarna
Upptäckten och förklaringen av den bråktalskvantiserade Halleffekten 1982-83 kan sägas utgöra ett indirekt påvisande av den nya kvantvätskan och dess bråktalsladdade kvasipartiklar. Nyligen har flera forskargrupper lyckats direkt observera dessa nya partiklar (se litteraturförteckningen). Detta har bland annat skett i experiment där mycket svaga variationer i en strömkrets kunnat hänföras till att enskilda kvasipartiklar flutit genom kretsen. Dessa mätningar, som kan liknas vid att under en hagelstorm urskilja ljudet från de enstaka hagelkornen och avgöra att de bara har bråkdelen av sin vanliga storlek, har möjliggjorts genom den häpnadsväckande teknikutveckling som skett inom mikroelektroniken sedan årets tre pristagare gjorde sina banbrytande insatser. Mätningarna kan sägas utgöra den slutgiltiga verifikationen av deras upptäckt.
| Lästips |
| Additional background material on the Nobel Prize in Physics 1998 [pdf]. |
| Splitting the electron, by B. Daviss, New Scientist, 31 January 1998, p. 36. |
| Fractionally charged quasiparticles signal their presence with noise, by G.P. Collins, Physics Today, November 1997, p. 17. |
| When the electron falls apart, by P.W. Anderson, Physics Today, October 1997, p. 42. |
| Electrons in flatland, by S. Kivelson, D.H. Lee and S.C. Zhang, Scientific American, March 1996, p. 64. |
| Composite Fermions: New particles in the fractional quantum Hall effect, by H. Störmer and D. Tsui, Physics News in 1994, American Institute of Physics 1995, p. 33. |
| Anyoner, av Hans Hansson och Anders Karlhede. I Svenska Fysikersamfundets årsbok Kosmos 1994. |
| Kondenserad materias fysik – oväntade upptäckter och nya vägar, av Mats Jonson, Bengt Lundqvist och Stig Lundqvist. I Svenska Fysikersamfundets årsbok Kosmos 1991. |
| The fractional quantum Hall effect, by J.P. Eisenstein and H.L. Stormer, Science, 22 June 1990, p. 1510. |
| Nobelpriset i fysik 1985, av Olof Beckman. I Svenska Fysikersamfundets årsbok Kosmos 1986. |
| Kvant-Hall-effekten – ett möte mellan makrokosmos och mikrokosmos, av Mats Jonson. I Fångad av forskning, Naturvetenskapliga forskningsrådets årsbok 1984. |
| Uppslagsord i Nationalencyklopedin. |
Robert B. Laughlin
född 1950 i Visalia, CA, USA. Amerikansk medborgare. Doktorsgrad i fysik 1979 vid Massachusetts Institute of Technology, Cambridge, USA. Professor i fysik vid Stanford University sedan 1989. Laughlin har bl.a. erhållit Oliver E. Buckley Prize av American Physical Society 1986 och Franklininstitutets medalj 1998 för sina arbeten rörande den bråktalskvantiserade Halleffekten.
Professor Robert B. Laughlin
Department of Physics, Varian Bldg
Stanford University
Stanford, CA 94305-4060
USA
Horst L. Störmer
född 1949 i Frankfurt/Main. Doktorsgrad i fysik 1977 vid Universität Stuttgart i Tyskland. Föreståndare för Physical Research Laboratory, Bell Laboratories 1992-97. Professor vid Columbia University, New York, och adjungerad föreståndare för fysik vid Lucent Technologies’ Bell Labs sedan 1998. Störmer har bl.a. erhållit Oliver E. Buckley Prize av American Physical Society 1984 och Franklininstitutets medalj 1998 för sina arbeten rörande den bråktalskvantiserade Halleffekten.
Professor Horst L. Störmer
Physics Department
Columbia University
New York, NY 10027
USA
Daniel C. Tsui
född 1939 i Henan, Kina. Amerikansk medborgare. Doktorsgrad i fysik 1967 vid University of Chicago, USA. Professor vid Princeton University sedan 1982. Tsui har bl.a. erhållit Oliver E. Buckley Prize av American Physical Society 1984 och Franklininstitutets medalj 1998 för sina arbeten rörande den bråktalskvantiserade Halleffekten.
Professor Daniel C. Tsui
Department of Electrical Engineering
Princeton University
PO Box 5263
Princeton, NJ 08544
USA
Nobel Prizes and laureates
Six prizes were awarded for achievements that have conferred the greatest benefit to humankind. The 14 laureates' work and discoveries range from quantum tunnelling to promoting democratic rights.
See them all presented here.
