Communiqué de presse: Le Prix Nobel de Physique de 1999
English
German
French
Swedish

12 Octobre 1999
L’Académie Royal des Sciences de Suède a attribué le Prix Nobel de Physique de l’année 1999 collectivement aux
Professeur Gerardus ‘t Hooft, Université d’Utrecht, Utrecht, Pays-Bas, et
Professeur émérite Martinus J.G. Veltman de University of Michigan, États-Unis, domicilié à Bilthoven, Pays-Bas.
Les deux chercheurs reçoivent le Prix Nobel pour avoir fourni à la théorie de la physique des particules une base mathématique plus solide. Il ont notamment montré comment utiliser la théorie pour préciser les calculs de grandeurs physiques mesurables. Des expériences dans les accélérateurs de particules en Europe et aux Etats-Unis ont récemment confirmé de nombreux résultats calculés.
Motivation de l’Académie des Sciences:
«pour leur travaux déterminants sur la structure quantique dans la théorie d’interaction électrofaible de la physique»
Théorie de la physique des particules sur une base mathématique plus solide
Les objets de notre environnement quotidien sont tous constitués d’atomes, eux-mêmes constitués d’électrons et de noyaux atomiques. Ceux-ci sont à leur tour composés de protons et de neutrons, eux-mêmes constitués de quarks. L’étude de la matière au niveau de ces éléments internes exige des accélérateurs puissants. Les premiers remontent aux années 1950 et marquent la naissance de la physique des particules moderne. Pour la première fois, les chercheurs réussirent alors à provoquer, sous une forme contrôlée, des collisions de particules atomiques hautement énergétiques. C’est ainsi que les physiciens observèrent l’apparition de nouvelles particules et identifièrent les forces qui agissent entre elles.
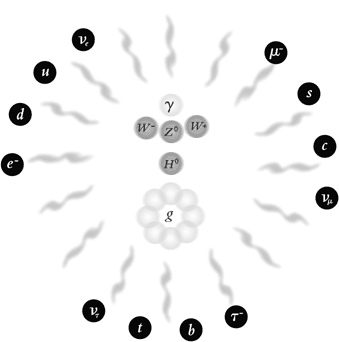
C’est aussi dans les années 1950 que fut formulée une première version de la théorie moderne qui, après de nombreuses années de perfectionnement, a finalement donné naissance au modèle standard au sein de la physique des particules. Selon ce modèle, toutes les particules élémentaires, regroupées dans trois familles de quarks et de leptons, interagissent à l’aide d’un certain nombre de particules médiatrices pour les forces fortes et électrofaibles (voir Figure 1).
La base théorique du modèle standard était initialement incomplète du point de vue mathématique et il n’était même pas certain qu’elle fût applicable à des calculs détaillés sur des grandeurs physiques mesurables. Cette année, Gerardus ‘t Hooft et Martinus J.G. Veltman sont récompensés par le Prix Nobel pour avoir fourni à cette théorie mathématique une base plus solide. Les chercheurs disposent désormais d’un édifice théorique qui peut leur servir, entre autres, à prédire les propriétés des nouvelles particules.
 |
|
Fig. 1. Les particules fondamentales de la matière sont six leptons et six quarks. Dans le modèle standard de la physique des particules, les forces entre ces éléments sont décrites par des théories quantiques des champs qui toutes sont des types de théories de jauge non abéliennes. Selon celles-ci, les forces électrofaibles sont transmises par quatre particules médiatrices. Ce sont le photon de masse nulle (gamma) et les trois particules lourdes W+, W – et Z0. La force forte est transmise par huit «gluons» g de masse nulle. En plus de ces douze particules médiatrices, la théorie prédit également l’existence d’une particule de champ très lourde, la particule de Higgs H0 dont le champ engendre toutes les masses des particules. |
Nouvelle dénomination d’une ancienne théorie
Les modèles théoriques modernes exploités aujourd’hui dans le modèle standard de la physique des particules et qui décrivent l’interaction entre les particules sont appelés
théories de jauge. Le nom jauge définit une propriété spécifique chez ces théories, la symétrie de jauge, considérée par de nombreux chercheurs comme l’une des propriétés les plus fondamentales de la physique. Mais dès les années 1860, l’Ecossais James Clerk Maxwell formula une théorie applicable à l’électromagnétisme qui, selon la terminologie moderne, est une théorie de jauge. Sa théorie, encore viable aujourd’hui, unifiait l’électricité au magnétisme et prédisait, entre autres, l’existence d’ondes hertziennes.
Il est possible d’illustrer le concept de la symétrie de jauge de la façon suivante: les champs électriques et magnétiques peuvent être exprimés à l’aide de fonctions potentielles. Celles-ci peuvent être échangées (transformation de jauge) selon un certain modèle sans provoquer la modification du champ. La transformation la plus simple consiste à additionner une constante au potentiel électrique. Pour les grandeurs physiques mesurables, ceci illustre une loi bien connue. Il est possible de calculer le potentiel électrique à partir d’un point zéro de l’espace-temps choisi arbitrairement: on fait varier le potentiel de jauge sans que le champ ne subisse la moindre modification. C’est ce qui explique qu’un écureuil puisse se promener sur une ligne à haute tension, sans risquer d’être électrocuté! Pour les physiciens, le fait que le point zéro puisse être déplacé de la sorte illustre une symétrie dans la théorie: la symétrie de jauge.
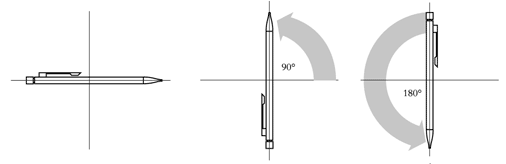
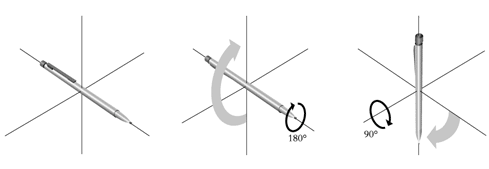
Lorsque l’on effectue deux transformations de jauge successivement, l’ordre dans lequel elles sont réalisées n’a aucune importance. L’interprétation généralement donnée à ce phénomène est que l’électromagnétisme est une théorie jauge abélienne, du nom du mathématicien Niels Henrik Abel, 1802-29. (Une illustration simple des transformations abéliennes sont les rotations dans le plan. Essayons de l’illustrer à l’aide d’un crayon! Voir Figure 2a)
Fig. 2a) Les rotations dans un plan bidimensionnel constituent un exemple de groupe de transformations abéliennes.
|
Posons un crayon sur une table, |
faisons-lui d’abord effectuer une rotation de 90o |
et puis une de 180o dans le même sens. |
|
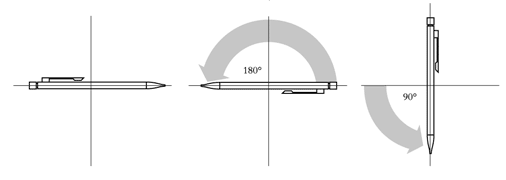
Inversons maintenant l’ordre des rotations: |
et faisons effectuer au crayon d’abord une rotation de 180o |
et faisons effectuer au crayon d’abord une rotation de 180o |
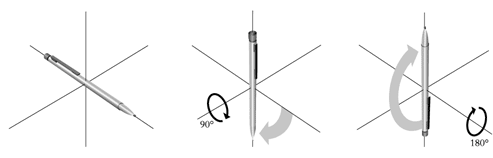
Fig. 2b) Les rotations dans l’espace tridimensionnel constituent un exemple de groupe de transformations non abéliennes.
|
Tenons d’abord un crayon à |
Faisons-lui ensuite effectuer une rotation de 90o de sorte qu’il pointe vers le sol.. |
Tournons-le ensuite de 180o afin qu’il pointe vers le haut. |
|
Inversons maintenant l’ordre des rotations: |
Effectuons d’abord la rotation à 180o (ce qui ne change pas la direction de la pointe mais pro-voque la rotation du crayon d’un demi-tour sur lui-même). |
Effectuons la rotation à 90o (le crayon pointe alors vers le sol). Le résultat est tout à fait différent! |
La mécanique quantique pose des problèmes
Dès que la mécanique quantique fut formulée dans les années 1925, les chercheurs entreprirent d’associer les fonctions ondulatoires de la mécanique quantique et le champ électromagnétique dans une théorie quantique des champs. Mais les chercheurs se heurtèrent à des difficultés! La nouvelle électrodynamique quantique se révélait complexe et quand on effectuait des calculs, les résultats obtenus étaient absurdes. Ceci était en partie dû à la théorie quantique qui prédit que le champ électromagnétique proche d’un électron ou d’un proton, par exemple, peut spontanément engendrer des myriades de paires de particules et d’antiparticules de longévité très brève, les particules virtuelles (voir Figure 3). Un système constitué d’un seul électron devenait subitement un problème relevant d’une multitude de particules.
Ce problème fut résolu dans les années 1940 par Sin-Itiro Tomonaga, Julian Schwinger et Richard P. Feynman (qui obtint le Prix Nobel en 1965 pour ses travaux). La méthode développée par ces trois chercheurs s’appelle «renormalisation». En simplifiant, on peut dire que cette approche consiste à observer les particules individuelles «à une certaine distance» Ainsi, il n’est pas nécessaire de considérer les paires de particules virtuelles individuellement : il suffit de laisser le « nuage » formé de paires de particules virtuelles ombrager la particule centrale initiale. Ainsi, celle-ci se caractérise, entre autres, par une nouvelle charge et une nouvelle masse. En utilisant la terminologie moderne, on peut dire que Tomonaga, Schwinger et Feynman renormèrent une théorie de jauge abélienne.
Ces derniers temps, les chercheurs ont testé l’électrodynamique quantique avec une précision plus grande que pour toute autre théorie sur les grandeurs physiques mesurables. Par exemple, Hans Dehmelt (Prix Nobel de Physique 1989), a réussi, dans un piège ionique, à mesurer le magnétisme de l’électron avec une précision de 12 chiffres. Les chercheurs ont comparé les 10 premiers chiffres aux résultats des calculs: la concordance était parfaite!
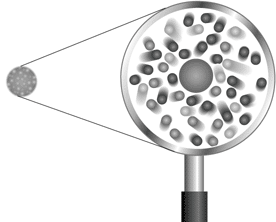
Fig. 3. Selon le théorie quantique des champs, une particule de grandeur physique mesurable réelle se compose d’une particule centrale «nue», enrobée d’un manteau nuageux de «particules virtuelles» de longévité très brève.
Unification des interactions électromagnétique et faible
La découverte et l’étude de la radioactivité relayées par l’évolution de la physique nucléaire au cours de la première moitié du 20e siècle, donnèrent naissance, entre autres, aux notions d’interaction forte et faible. Pour les expliquer de façon très simplifiée, on peut dire que l’interaction forte retient ensemble les éléments du noyau atomique alors que l’interaction faible permet la désintégration radioactive de certains d’entre eux. Dans les années 1930 déjà, les chercheurs formulèrent une première théorie quantique des champs pour l’interaction faible. Ce modèle théorique se heurta à des difficultés encore plus sérieuses que ceux qu’avait connu l’électrodynamique quantique. Pas même la méthode de renormalisation développée par Tomonaga, Schwinger et Feynman ne pouvait les surmonter.
Mais au milieu des années 50, plusieurs chercheurs formulèrent un premier exemple de théorie quantique des champs présentant de nouvelles propriétés : une théorie de jauge non abélienne. A la différence de la variante abélienne, selon laquelle les transformations de jauge peuvent être réalisées indépendamment de leur ordre de succession, les résultats de la théorie non abélienne dépendent de cet ordre. Ceci confère à la théorie une structure mathématique plus complexe, mais ouvre par ailleurs de nouvelles perspectives. (Les rotations dans l’espace sont un exemple simple de transformations non abéliennes. Expérimentons avec un crayon! Voir Figure 2b)
Il fallut attendre les années 1960 pour que les nouvelles possibilités offertes par la théorie soient pleinement exploitées. Plusieurs équipes de chercheurs contribuèrent alors au développement d’une théorie de jauge non abélienne qui combine l’interaction électromagnétique et l’interaction faible en une interaction électrofaible (Prix Nobel 1979 attribué à Sheldon H. Glashow, Abdus Salam et Steven Weinberg). Cette théorie quantique des champs prédisait, entre autres, l’existence des nouvelles particules W et Z. Ces dernières furent mises en évidence en 1983 au CERN, le laboratoire d’accélération de particules à Genève (Prix Nobel 1984 décerné à Carlo Rubbia et Simon van der Meer).
L’histoire se répète
La théorie de l’interaction électrofaible développée pendant les années 1960 constituait certainement un grand pas en avant mais la communauté scientifique l’accepta difficilement dans un premier temps. Lorsqu’ils tentaient de l’utiliser pour effectuer des calculs plus précis des propriétés des nouvelles particules W et Z (ainsi que de nombreuses autres grandeurs physiques mesurables), les chercheurs obtenaient des résultats absurdes. Cette situation rappelait celle des années 30, avant que Tomonoga, Schwinger et Feynman ne réussissent à renormer l’électrodynamique quantique. De nombreux chercheurs exprimaient leur pessimisme sur les perspectives offertes par cette théorie.
Martinus J.G. Veltman appartenait au nombre de physiciens espérant encore réussir à renormer les théories de jauge non abéliennes. A la fin des années 60, il venait d’être nommé professeur à l’Université d’Utrecht. Veltman avait élaboré un logiciel, Schoonschip, qui effectuait symboliquement les simplifications algébriques d’expressions complexes engendrées par toutes les théories quantiques des champs lorsque l’on entreprenait des calculs quantitatifs. 20 ans auparavant, Feynman avait bien systématisé le problème des calculs et introduit les diagrammes dit diagrammes de Feynman, très vite adoptés par le monde des chercheurs. Mais à cette époque, les ordinateurs n’existaient pas. Veltman était pleinement convaincu qu’il trouverait un moyen d’effectuer la renormalisation, et son logiciel constituait une pierre angulaire dans le vaste travail consistant à tester les différentes idées.
Au printemps 1969, Veltman accueillit un nouvel élève de 22 ans nommé Gerardus ‘t Hooft, qui avait exprimé le désir d’étudier la physique des hautes énergies. Après avoir rédigé un premier mémoire, ‘t Hooft fut admis à préparer sa thèse de doctorat l’automne de la même année. Sa tâche consistait à participer à la recherche d’une méthode pour réaliser la renormalisation des théories de jauge non abéliennes. ‘t Hooft réussit au-delà de toute espérances et publia dès 1971 deux articles représentant une percée dans le programme de recherche.
A l’aide du logiciel de Veltman, les chercheurs procédèrent à la vérification des résultats partiels de ‘t Hooft et ils développèrent ensemble une méthode de calcul détaillée fonctionnelle. Ainsi, la théorie de jauge d’interaction électrofaible non abélienne devenait maintenant un édifice théorique utilisable, qui, tout comme pour l’électrodynamique quantique 20 auparavant, allait permettre d’effectuer des calculs précis.
Vérification des postulats théoriques
Ainsi qu’il a été décrit ci-dessus, la théorie électrofaible prédisait dès son origine l’existence des nouvelles particules W et Z. Mais les travaux de Veltman et de ‘t Hooft ouvrirent la voie à des calculs de grandeurs physicales plus précises dans lesquelles les propriétés de W et Z jouaient un rôle. Dans l’accélérateur LEP du CERN, les scientifiques créent depuis une dizaine d’années d’importantes quantités de particules W et Z dans des conditions contrôlables. Les comparaisons entre les mesures et les calculs ont constamment montré une grande concordance, confirmant ainsi les postulats théoriques.
Une quantité particulière se laissait appréhender par la méthode de calcul de Veltman et de ‘t Hooft à partir des résultats obtenus au LEP: la masse du quark top, le plus lourd des deux quarks appartenant à la troisième famille du modèle standard. Ce quark fut directement identifié la première fois en 1995 au Fermilab américain, mais sa masse avait était prédite déjà plusieurs années auparavant. Là encore, la concordance entre l’expérience et la théorie donna satisfaction.
A quand la prochaine grande découverte?
Un élément important de l’édifice théorique élaborée par Veltman et ‘t Hooft est une particule non encore identifiée, baptisée particule de Higgs (voir Figure 1). Tout comme pour d’autres particules dont l’existence a été prédite par les arguments théoriques puis identifiées expérimentalement, les chercheurs attendent maintenant l’observation directe de la particule de Higgs. Par des calculs comparables à ceux effectués pour déterminer la masse du quark top, on sait qu’il y a une chance pour que l’un des accélérateurs existants produisent quelques particules de Higgs. Mais le LHC (Large Hadron Collider ) du CERN, le seul accélérateur suffisamment puissant pour permettre l’étude détaillée de la particule est actuellement en construction. Alors les chercheurs devront faire preuve d’un peu de patience car sa mise en service n’est prévue que pour l’an 2005!
| Liste d’ouvrages conseillés |
| Additional background material on the Nobel Prizes in Physics 1999, by Professor Cecilia Jarlskog, the Royal Swedish Academy of Sciences (pdf). |
| In search of the Ultimate Building Blocks by Gerard ‘t Hooft, Cambridge University Press 1997. |
| The Higgs boson by Martinus J.G. Veltman, Scientific American, November 1986, p. 88. |
| An Elementary Primer for Gauge Theory by K. Moriyasu, World Scientific Publishing 1983. |
| Gauge Theories of the Forces between Elementary Particles by Gerard ‘t Hooft, Scientific American, June 1980, p. 90. |
Gerardus ‘t Hooft
né en 1946 à Den Helder, Pays-Bas. De nationalité néerlandaise. Doctorat de physique en 1972 à l’Université d’Utrecht. Professeur de physique à l’Université d’Utrecht depuis 1977. ‘t Hooft a, entre autres, reçu le Dannie Heineman Prize de l’American Physical Society en 1979 et le prix Wolf en 1982 pour ses travaux sur la renormalisation des théories de jauge. Il est membre de l’Académie des Sciences des Pays-Bas depuis 1982.
Professor Gerardus ‘t Hooft
Spinoza Instituut
Leuvenlaan 4
Postbus 80.195
3508 TD Utrecht
The Netherlands
Martinus J. G. Veltman
Né en 1931 aux Pays-Bas. De nationalité néerlandaise. Doctorat de physique en 1963 à l’Université d’Utrecht. Professeur de physique à l’Université d’Utrecht de 1966 à 1981 puis à l’Université du Michigan, Ann Arbor à partir de 1981 (maintenant retraité). Veltman a, entre autres distinctions, reçu en 1983 le High Energy and Particle Physics Prize de l’European Physical Society pour ses études sur la renormalisation des théories de jauge. Il est membre de l’Académie des Sciences des Pays-Bas depuis 1981.
Professor Martinus J. G. Veltman
Schubertlaan 15
3723 LM Bilthoven
The Netherlands
Le montant du prix s’élève à SEK 7,900,000.
Nobel Prizes and laureates
Six prizes were awarded for achievements that have conferred the greatest benefit to humankind. The 14 laureates' work and discoveries range from quantum tunnelling to promoting democratic rights.
See them all presented here.
