Popular science background:
They used physics to find patterns in information (pdf)

Populärvetenskaplig information:
De använde fysiken för att hitta mönster i information (pdf)

The Nobel Prize in Physics 2024

This year’s laureates used tools from physics to construct methods that helped lay the foundation for today’s powerful machine learning. John Hopfield created a structure that can store and reconstruct information. Geoffrey Hinton invented a method that can independently discover properties in data and which has become important for the large artificial neural networks now in use.

They used physics to find patterns in information

Many people have experienced how computers can translate between languages, interpret images and even conduct reasonable conversations. What is perhaps less well known is that this type of technology has long been important for research, including the sorting and analysis of vast amounts of data. The development of machine learning has exploded over the past fifteen to twenty years and utilises a structure called an artificial neural network. Nowadays, when we talk about artificial intelligence, this is often the type of technology we mean.

Although computers cannot think, machines can now mimic functions such as memory and learning. This year’s laureates in physics have helped make this possible. Using fundamental concepts and methods from physics, they have developed technologies that use structures in networks to process information.

Machine learning differs from traditional software, which works like a type of recipe. The software receives data, which is processed according to a clear description and produces the results, much like when someone collects ingredients and processes them by following a recipe, producing a cake. Instead of this, in machine learning the computer learns by example, enabling it to tackle problems that are too vague and complicated to be managed by step by step instructions. One example is interpreting a picture to identify the objects in it.

Mimics the brain

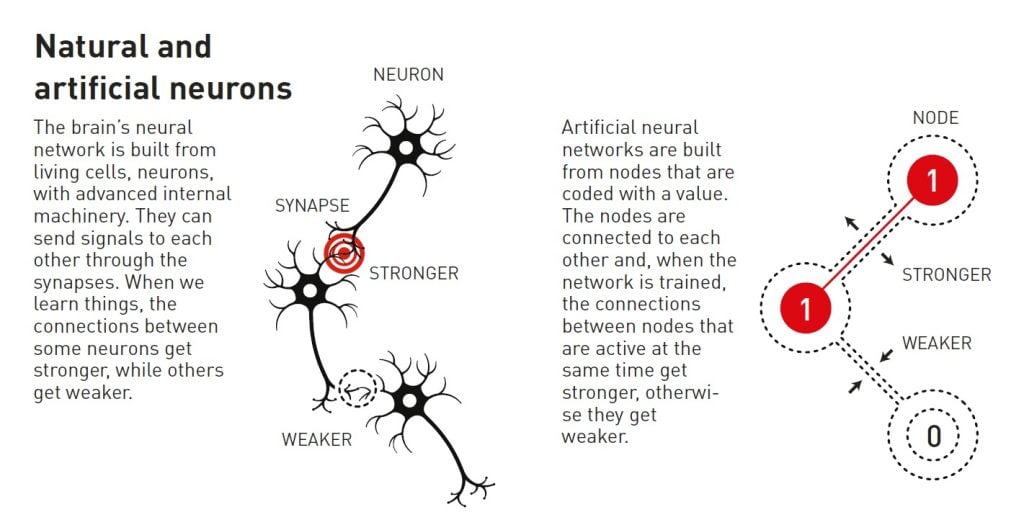
An artificial neural network processes information using the entire network structure. The inspiration initially came from the desire to understand how the brain works. In the 1940s, researchers had started to reason around the mathematics that underlies the brain’s network of neurons and synapses. Another piece of the puzzle came from psychology, thanks to neuroscientist Donald Hebb’s hypothesis about how learning occurs because connections between neurons are reinforced when they work together.

Later, these ideas were followed by attempts to recreate how the brain’s network functions by building artificial neural networks as computer simulations. In these, the brain’s neurons are mimicked by nodes that are given different values, and the synapses are represented by connections between the nodes that can be made stronger or weaker. Donald Hebb’s hypothesis is still used as one of the basic rules for updating artificial networks through a process called training.

At the end of the 1960s, some discouraging theoretical results caused many researchers to suspect that these neural networks would never be of any real use. However, interest in artificial neural networks was reawakened in the 1980s, when several important ideas made an impact, including work by this year’s laureates.

Associative memory

Imagine that you are trying to remember a fairly unusual word that you rarely use, such as one for that sloping floor often found in cinemas and lecture halls. You search your memory. It’s something like ramp… perhaps rad…ial? No, not that. Rake, that’s it!

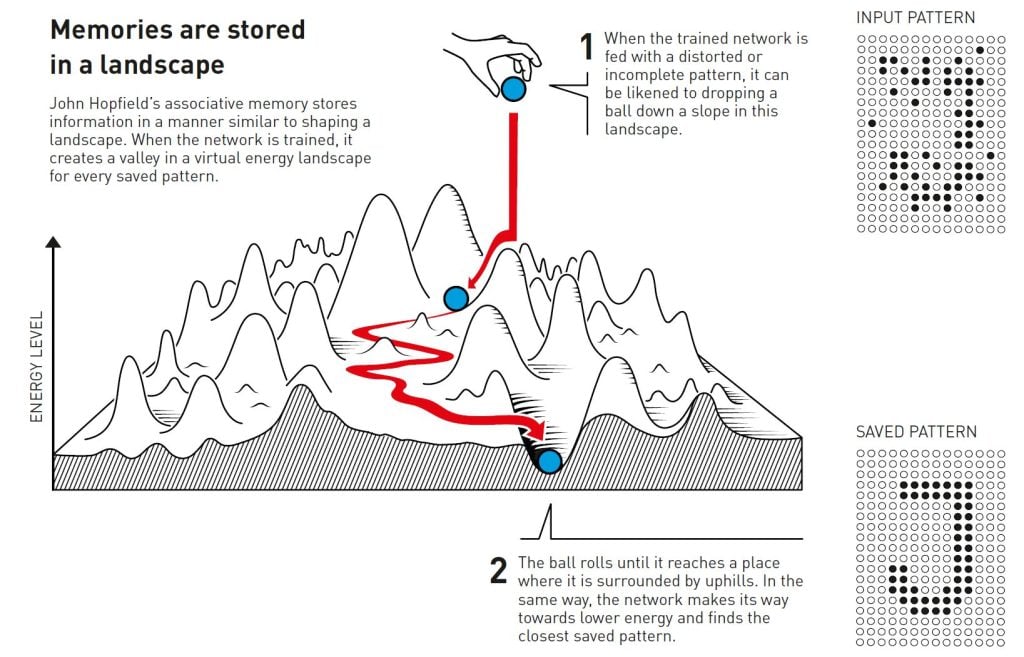
This process of searching through similar words to find the right one is reminiscent of the associative memory that the physicist John Hopfield discovered in 1982. The Hopfield network can store patterns and has a method for recreating them. When the network is given an incomplete or slightly distorted pattern, the method can find the stored pattern that is most similar.

Hopfield had previously used his background in physics to explore theoretical problems in molecular biology. When he was invited to a meeting about neuroscience he encountered research into the structure of the brain. He was fascinated by what he learned and started to think about the dynamics of simple neural networks. When neurons act together, they can give rise to new and powerful characteristics that are not apparent to someone who only looks at the network’s separate components.

In 1980, Hopfield left his position at Princeton University, where his research interests had taken him outside the areas in which his colleagues in physics worked, and moved across the continent. He had accepted the offer of a professorship in chemistry and biology at Caltech (California Institute of Technology) in Pasadena, southern California. There, he had access to computer resources that he could use for free experimentation and to develop his ideas about neural networks.

However, he did not abandon his foundation in physics, where he found inspiration for his under­standing of how systems with many small components that work together can give rise to new and interesting phenomena. He particularly benefitted from having learned about magnetic materials that have special characteristics thanks to their atomic spin – a property that makes each atom a tiny magnet. The spins of neighbouring atoms affect each other; this can allow domains to form with spin in the same direction. He was able to make a model network with nodes and connections by using the physics that describes how materials develop when spins influence each other.

The network saves images in a landscape

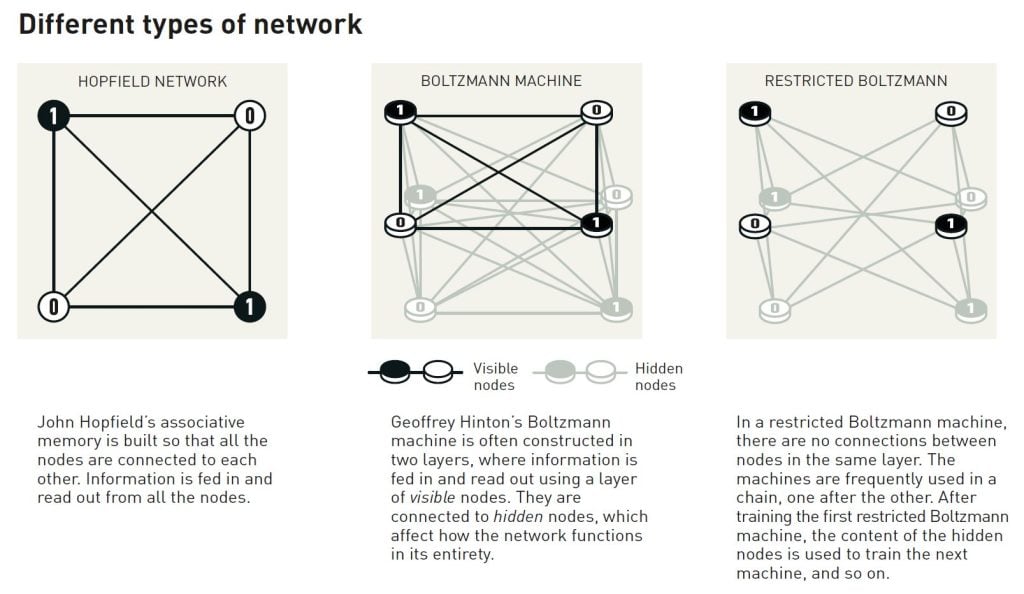
The network that Hopfield built has nodes that are all joined together via connections of different strengths. Each node can store an individual value – in Hopfield’s first work this could either be 0 or 1, like the pixels in a black and white picture.

Hopfield described the overall state of the network with a property that is equivalent to the energy in the spin system found in physics; the energy is calculated using a formula that uses all the values of the nodes and all the strengths of the connections between them. The Hopfield network is programmed by an image being fed to the nodes, which are given the value of black (0) or white (1). The network’s connections are then adjusted using the energy formula, so that the saved image gets low energy. When another pattern is fed into the network, there is a rule for going through the nodes one by one and checking whether the network has lower energy if the value of that node is changed. If it turns out that energy is reduced if a black pixel is white instead, it changes colour. This procedure continues until it is impossible to find any further improvements. When this point is reached, the network has often reproduced the original image on which it was trained.

This may not appear so remarkable if you only save one pattern. Perhaps you are wondering why you don’t just save the image itself and compare it to another image being tested, but Hopfield’s method is special because several pictures can be saved at the same time and the network can usually differentiate between them.

Hopfield likened searching the network for a saved state to rolling a ball through a landscape of peaks and valleys, with friction that slows its movement. If the ball is dropped in a particular location, it will roll into the nearest valley and stop there. If the network is given a pattern that is close to one of the saved patterns it will, in the same way, keep moving forward until it ends up at the bottom of a valley in the energy landscape, thus finding the closest pattern in its memory.

The Hopfield network can be used to recreate data that contains noise or which has been partially erased.

Hopfield and others have continued to develop the details of how the Hopfield network functions, including nodes that can store any value, not just zero or one. If you think about nodes as pixels in a picture, they can have different colours, not just black or white. Improved methods have made it possible to save more pictures and to differentiate between them even when they are quite similar. It is just as possible to identify or reconstruct any information at all, provided it is built from many data points.

Classification using nineteenth-century physics

Remembering an image is one thing, but interpreting what it depicts requires a little more.

Even very young children can point at different animals and confidently say whether it is a dog, a cat, or a squirrel. They might get it wrong occasionally, but fairly soon they are correct almost all the time. A child can learn this even without seeing any diagrams or explanations of concepts such as species or mammal. After encountering a few examples of each type of animal, the different categories fall into place in the child’s head. People learn to recognise a cat, or understand a word, or enter a room and notice that something has changed, by experiencing the environment around them.

When Hopfield published his article on associative memory, Geoffrey Hinton was working at Carnegie Mellon University in Pittsburgh, USA. He had previously studied experimental psychology and artificial intelligence in England and Scotland and was wondering whether machines could learn to process patterns in a similar way to humans, finding their own categories for sorting and interpreting information. Along with his colleague, Terrence Sejnowski, Hinton started from the Hopfield network and expanded it to build something new, using ideas from statistical physics.

Statistical physics describes systems that are composed of many similar elements, such as molecules in a gas. It is difficult, or impossible, to track all the separate molecules in the gas, but it is possible to consider them collectively to determine the gas’ overarching properties like pressure or temperature. There are many potential ways for gas molecules to spread through its volume at individual speeds and still result in the same collective properties.

The states in which the individual components can jointly exist can be analysed using statistical physics, and the probability of them occurring calculated. Some states are more probable than others; this depends on the amount of available energy, which is described in an equation by the nineteenth-century physicist Ludwig Boltzmann. Hinton’s network utilised that equation, and the method was published in 1985 under the striking name of the Boltzmann machine.

Recognising new examples of the same type

The Boltzmann machine is commonly used with two different types of nodes. Information is fed to one group, which are called visible nodes. The other nodes form a hidden layer. The hidden nodes’ values and connections also contribute to the energy of the network as a whole.

The machine is run by applying a rule for updating the values of the nodes one at a time. Eventually the machine will enter a state in which the nodes’ pattern can change, but the properties of the network as a whole remain the same. Each possible pattern will then have a specific probability that is determined by the network’s energy according to Boltzmann’s equation. When the machine stops it has created a new pattern, which makes the Boltzmann machine an early example of a generative model.

The Boltzmann machine can learn – not from instructions, but from being given examples. It is trained by updating the values in the network’s connections so that the example patterns, which were fed to the visible nodes when it was trained, have the highest possible probability of occurring when the machine is run. If the same pattern is repeated several times during this training, the probability for this pattern is even higher. Training also affects the probability of outputting new patterns that resemble the examples on which the machine was trained.

A trained Boltzmann machine can recognise familiar traits in information it has not previously seen. Imagine meeting a friend’s sibling, and you can immediately see that they must be related. In a similar way, the Boltzmann machine can recognise an entirely new example if it belongs to a category found in the training material, and differentiate it from material that is dissimilar.

In its original form, the Boltzmann machine is fairly inefficient and takes a long time to find solutions. Things become more interesting when it is developed in various ways, which Hinton has continued to explore. Later versions have been thinned out, as the connections between some of the units have been removed. It turns out that this may make the machine more efficient.

During the 1990s, many researchers lost interest in artificial neural networks, but Hinton was one of those who continued to work in the field. He also helped start the new explosion of exciting results; in 2006 he and his colleagues Simon Osindero, Yee Whye Teh and Ruslan Salakhutdinov developed a method for pretraining a network with a series of Boltzmann machines in layers, one on top of the other. This pretraining gave the connections in the network a better starting point, which optimised its training to recognise elements in pictures.

The Boltzmann machine is often used as part of a larger network. For example, it can be used to recommend films or television series based on the viewer’s preferences.

Machine learning – today and tomorrow

Thanks to their work from the 1980s and onward, John Hopfield and Geoffrey Hinton have helped lay the foundation for the machine learning revolution that started around 2010.

The development we are now witnessing has been made possible through access to the vast amounts of data that can be used to train networks, and through the enormous increase in computing power. Today’s artificial neural networks are often enormous and constructed from many layers. These are called deep neural networks and the way they are trained is called deep learning.

A quick glance at Hopfield’s article on associative memory, from 1982, provides some perspective on this development. In it, he used a network with 30 nodes. If all the nodes are connected to each other, there are 435 connections. The nodes have their values, the connections have different strengths and, in total, there are fewer than 500 parameters to keep track of. He also tried a network with 100 nodes, but this was too complicated, given the computer he was using at the time. We can compare this to the large language models of today, which are built as networks that can contain more than one trillion parameters (one million millions).

Many researchers are now developing machine learning’s areas of application. Which will be the most viable remains to be seen, while there is also wide-ranging discussion on the ethical issues that surround the development and use of this technology.

Because physics has contributed tools for the development of machine learning, it is interesting to see how physics, as a research field, is also benefitting from artificial neural networks. Machine learning has long been used in areas we may be familiar with from previous Nobel Prizes in Physics. These include the use of machine learning to sift through and process the vast amounts of data necessary to discover the Higgs particle. Other applications include reducing noise in measurements of the gravitational waves from colliding black holes, or the search for exoplanets.

In recent years, this technology has also begun to be used when calculating and predicting the properties of molecules and materials – such as calculating protein molecules’ structure, which determines their function, or working out which new versions of a material may have the best properties for use in more efficient solar cells.

Further reading

Additional information on this year’s prizes, including a scientific background in English, is available on the website of the Royal Swedish Academy of Sciences, www.kva.se, and at www.nobelprize.org, where you can watch video from the press conferences, the Nobel Lectures and more. Information on exhibitions and activities related to the Nobel Prizes and the Prize in Economic Sciences is available at www.nobelprizemuseum.se.

The Royal Swedish Academy of Sciences has decided to award the Nobel Prize in Physics 2024 to

JOHN J. HOPFIELD
Born 1933 in Chicago, IL, USA. PhD 1958 from Cornell University, Ithaca, NY, USA. Professor at Princeton University, NJ, USA.

GEOFFREY HINTON
Born 1947 in London, UK. PhD 1978 from The University of Edinburgh, UK. Professor at University of Toronto, Canada.

“for foundational discoveries and inventions that enable machine learning with artificial neural networks”

Science Editors: Ulf Danielsson, Olle Eriksson, Anders Irbäck, and Ellen Moons, the Nobel Committee for Physics
Text: Anna Davour
Translator: Clare Barnes
Illustrations: Johan Jarnestad
Editor: Sara Gustavsson
© The Royal Swedish Academy of Sciences